[자료구조] AVL트리 (AVL Tree)

이진검색트리는 저장과 검색에 평균 Θ(log n)시간이 소요되지만 운이 나쁘면 트리의 모양이 균형을 잘 이루지 못한다. 균형이 많이 깨지면 Θ(n)에 근접한 시간이 소요될 수도 있다. 그래서 고안해 낸 것이 **균형잡힌 이진검색트리(Balanced Binary Search Tree)**이다. 균형잡힌 이진검색트리는 최악의 경우에도 이진트리의 균형이 잘 맞도록 유지한다. 균형잡힌 이진검색트리로 대표적인 것은 AVL트리와 레드블랙트리다.

 

AVL Tree

Adelson-Velsky and Landis Tree

---

극단적으로는 n개의 노드가 크기 순으로 일렬로 늘어뜨려져 높이 또한 n이 되는 경우도 이진 탐색 트리에 해당된다. 결과적으로 이진 탐색 트리의 계산복잡성은 O(n)이 되는데, 이것으로는 탐색 속도가 O(logn)으로 빠른 이진 탐색을 계승했다고 보기 어렵다.

이진 트리의 높이가 항상 O(log n)이면, 탐색 트리 기능에 대해 O(log n)의 성능을 보장할 수 있다.

Worst-case의 높이가 O(log n)인 트리를 balanced tree라고 한다. balanced tree의 예로 이진탐색트리의 일종인 AVL Tree가 있다.

 

1. AVL Tree

• 이진트리
• 만약 T가 왼쪽, 오른쪽 서브트리로 TL과 TR을 가진 비어있지 않은 이진 트리라면, T는 AVL트리이다.
  • TL과 TR은 AVL 트리이며,
  • hL과 hR은 각각 TL과 TR의 높이일 떄, 다음과 같은 조건을 만족한다.

 

2. AVL Search Tree

: AVL Search Tree는 AVL트리이기도 한 이진 탐색 트리이다.

AVL 트리 : (a), (b) / AVL search tree : (b)

 

                                                

 

AVL Tree의 특징

• 노드가 n개인 AVL 트리의 높이는 O(log n)이다.
• 모든 n의 값에 대하여 n ≥ 0이면 AVL 트리가 존재한다.
• 노드가 n개인 AVL Search Tree는 O(height)=O(log n)시간에 탐색할 수 있다.
• 노드가 n개인 AVL Search Tree에 새 노드를 삽입하여 n+1개 노드의 AVL 트리를 만들 수 있고, 이 때의 삽입에 걸리는 시간은 O(log n)이다.
• n>0, 노드가 n개인 AVL Search Tree에서 노드를 삭제하면 노드가 n-1개인 AVL 트리가 되고, 삭제에 걸리는 시간은 O(log n)이다.

 

 

Balance Factor

균형 인수

---

• AVL tree는 일반적으로 linked representation을 사용하여 표현한다.
• 삽입 및 삭제를 용이하게 하기 위해 균형인수(**balance factor)**가 각 노드에 연결된다.
• 노드 x의 균형 인수인 **bf(x)**는 height(x→leftChild) – **height(x→rightChild)**로 정의된다.
• AVL 트리에서 각 노드의 균형 계수는 -1이나 0이나 1이어야 한다.

AVL Search Tree with Balance Factor

 

 

AVL Search Tree의 활용

---

📌 탐색

---

일반 이진 탐색 트리의 탐색 연산으로 수행한다.

• 시간 복잡도 : O(log n)

 

📌 삽입

---

AVL 탐색 트리에 요소를 삽입하다보면 트리의 균형이 맞지 않아 AVL트리가 아니게 될 수도 있다. 이렇듯 트리가 불균형 상태가 되면 균형을 회복하기 위해 트리를 조정해야 한다. 이 조정을 회전(rotation)이라고 한다.

Inserting into an AVL Search Tree

 

 Imbalance Types

---

      불균형 유형. 삽입 후, 노드 A의 균형 인수가 -2 또는 2일 때, 노드 A는 다음 네 가지 불균형 유형 중 하나이다.

      1) LL : 새 노드가 A의 왼쪽 하위 트리의 왼쪽 하위 트리에 있다.

      2) LR : 새 노드가 A의 왼쪽 하위 트리의 오른쪽 하위 트리에 있다.

      3) RR : 새 노드가 A의 오른쪽 하위 트리의 오른쪽 하위 트리에 있다.

      4) RL : 새 노드가 A의 오른쪽 하위 트리의 왼쪽 하위 트리에 있다.

 

👉🏻 (삽입 후) 불균형 AVL 트리의 균형을 맞추기 위해 LL, RR, LR, RL 회전 중 하나를 수행한다.

 

Rotation

---

1. Single Rotation

일반적인 경우의 single rotation은 노드A와 B의 위치를 바꾸어 주고 서브 트리들을 정리하면 균형 트리로 만들 수 있다.

Single Rotation

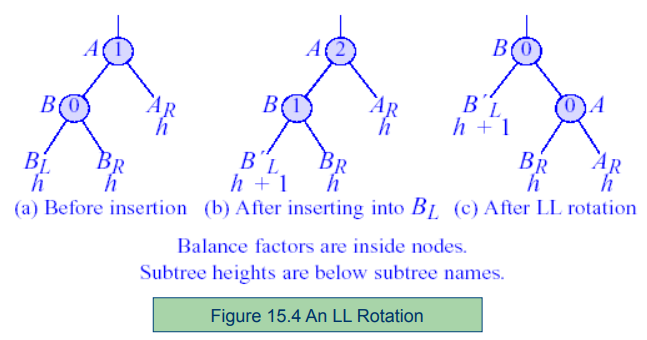
1) LL Rotation

루트노드를 자식노드의 오른쪽 서브트리로 붙이면 된다. 오른쪽으로 회전시키는 모양이다. 자식노드에 오른쪽 서브트리가 있을 수 있으므로 오른쪽 서브트리는 루트노드의 왼쪽 서브트리에 연결시킨다.

2) RR Rotation

루트노드를 자식노드의 왼쪽 서브트리로 붙이면 된다. 왼쪽으로 회전시키는 모양이다. 자식노드에 왼쪽 서브트리가 있을 수 있다. 이 왼쪽 서브트리를 루트 노드의 오른쪽 서브트리로 만든다.

 

2. Double Rotation

쉽게 설명하자면, Single Rotation을 두 번 한다고 생각하면 된다.

1) LR Rotation

    : 부분적 RR회전에 이어서 LL회전

 

2. RL Rotation

    : 부분적 LL회전에 이어서 RR회전

 

📌 삭제

---

• 삽입과 마찬가지로, 노드를 삭제해도 불균형이 발생할 수 있다.
• 삭제로 인한 균형 재조정에도 회전(Rotation)이 필요하다
• 삭제로 인한 불균형은 R0, R1, R-1, L0, L1, L-1로 분류된다.

• R1 Rotation

• R0 Rotation

• R-1 Rotation

 

 

참고자료

• https://designatedroom87.tistory.com/17
• https://slidesplayer.org/slide/16283436/