[자료구조] 이진탐색트리(Binary Search Tree)
💡 이진 탐색 트리는 이름에서 알 수 있듯이, 삽입이나 삭제보다는 탐색에 주 목적을 둔 자료구조이다.
Search Tree
탐색 트리
- skip lists와 hash table들과 같거나 그 이상의 성능을 가짐
- 사전을 구현하는 데에 이상적인 구조
- 순차적 또는 등급별 데이터 접근에 이상적
💡 빈출! 이진 트리와 이진 탐색 트리의 차이점
- 이진 트리 : 노드의 최대 Branch가 2인 트리
- 이진 탐색 트리 : 이진 트리에 추가적인 조건이 있는 트리
⇒ 조건 : 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있음.
Binary Search Tree
이진 탐색 트리

이진 탐색 트리는 트리가 비어있지 않은 경우 다음과 같은 속성을 만족한다.
- 모든 노드 x에 대하여,오른쪽 서브트리의 모든 key값은 노드 x의 key값보다 크다.
- 왼쪽 서브트리의 모든 key값은 노드 x의 key값보다 작다.
- 모든 노드는 서로 다른 유일한 key값을 가짐
- 왼쪽 서브 트리와 오른쪽 서브 트리도 이진 탐색 트리임
- 이진 탐색 트리를 중위 순회하면 오름차순으로 정렬된 값을 얻을 수 있음
구현
작업이 수행됨에 따라 이진 탐색 트리의 모양과 요소들의 수가 변하기 때문에, 일반적으로 linked representation을 사용하여 표현된다.
Python 구현 클래스 정의 및 초기화
class Node(object): # 먼저 Node 클래스를 정의
def __init__(self, data):
self.data = data
self.left = self.right = None # 초기화할 때는 데이터 값만 주어지고 좌우 노드는 비어있음
class BinarySearchTree(object):
def __init__(self):
self.root = None # 처음에는 비어 있는 트리로 초기화
탐색
루트부터 시작하며, key가 루트보다 작으면 왼쪽 하위 트리가 탐색되고 key가 루트보다 크면 오른쪽 하위 트리가 탐색된다. key가 루트와 같으면 검색이 성공적으로 종료된다.
- 루트가 NULL이면 탐색 트리가 트리가 비어 있어 탐색 실패
- 시간 복잡도 O(height)
Python 구현 : find() Method 재귀와 값의 대소관계 비교를 통해 구현할 수 있다.
class BinarySearchTree(object):
...
def find(self, key):
return self._find_value(self.root, key)
def _find_value(self, root, key):
if root is None or root.data == key:
return root is not None
elif key < root.data:
return self._find_value(root.left, key)
else:
return self._find_value(root.right, key)
삽입
- 이진 검색 트리에 새 요소 e를 삽입하려면 먼저 트리에서 탐색을 수행하여 key가 이미 존재하지 않는지 확인해야 한다.
- 탐색이 성공하면 삽입하지 않으며, 탐색에 실패하면 요소가 검색이 종료된 지점에 삽입된다.
💡 왜 그 지점에 삽입되는가?
탐색의 원리를 이해했으면 쉽다. 탐색 중 루트가 NULL으로 트리가 비어있는 경우 탐색에 실패하기 때문
- 시간 복잡도 O(height)
Python 구현 예시 : Insert Method
👉🏻 insert 7

재귀를 이용해서 구현하면 간단하다. 새로 추가할 원소의 값을 현재 노드의 값과 비교하여 왼쪽/오른쪽 중 알맞은 위치로 노드를 옮겨가면서 삽입 위치를 확인한다.
class BinarySearchTree(object):
...
def insert(self, data):
self.root = self._insert_value(self.root, data)
return self.root is not None
def _insert_value(self, node, data):
if node is None:
node = Node(data)
else:
if data <= node.data:
node.left = self._insert_value(node.left, data)
else:
node.right = self._insert_value(node.right, data)
return node
삭제
요소의 삭제는 세 가지 경우로 나누어 생각해볼 수 있다.
case 1 : 요소가 leaf에 있다.
👉🏻 Ex) delete key=7

case 2 : 요소가 차수 1의 노드에 있다 (즉, 비어 있지 않은 서브트리가 하나 존재).
👉🏻 delete key=40


case 3 : 요소가 차수 2의 노드에 있다 (즉, 비어 있지 않은 두 개의 서브트리가 존재).
👉🏻 Ex 1) delete key=10s
 |
|---|
| ▲ step 1 |
 |
| ▲ step 2. 왼쪽 서브트리에서 가장 큰 key로 대체 (또는 오른쪽 하위 트리에서 가장 작은 key로 대체) |
 |
| :--: |
| ▲ step 3. 가장 큰 key는 leaf 또는 차수 1인 노드에 있어야 한다. |
👉🏻 Ex 2) delete key=20
 |
|---|
| ▲ 왼쪽 서브트리의 가장 큰 key값으로 대체한다. |
💬 왼쪽 서브 트리에서 key가 가장 큰 노드(+ 오른쪽 서브 트리에서 key가 가장 작은 노드)는 0 또는 비어 있지 않은 서브 트리가 하나 있는 노드에 있어야 합니다.
💡 노드의 왼쪽 서브트리에서 key가 가장 큰 노드를 찾는 방법
서브 트리의 루트로 이동한 다음 오른쪽 자식의 포인터가 NULL인 노드에 도달할 때까지 계속 오른쪽 자식
포인터를 따라간다.
💡 노드의 오른쪽 서브트리에서 key가 가장 작은 노드를 찾는 방법
서브 트리의 루트로 이동한 다음 왼쪽 자식의 포인터가 NULL인 노드에 도달할 때까지 계속 왼쪽 자식
포인터를 따라간다.
- 시간복잡도 : O(height)
Python 구현 예시 : delete Method
class BinarySearchTree(object):
...
def delete(self, key):
self.root, deleted = self._delete_value(self.root, key)
return deleted
def _delete_value(self, node, key):
if node is None:
return node, False
deleted = False
if key == node.data:
deleted = True
if node.left and node.right:
# replace the node to the leftmost of node.right
parent, child = node, node.right
while child.left is not None:
parent, child = child, child.left
child.left = node.left
if parent != node:
parent.left = child.right
child.right = node.right
node = child
elif node.left or node.right:
node = node.left or node.right
else:
node = None
elif key < node.data:
node.left, deleted = self._delete_value(node.left, key)
else:
node.right, deleted = self._delete_value(node.right, key)
return node, deleted
Binary Search Tree의 시간복잡도
- 이진 트리의 좌우 균형이 맞는다면 탐색, 삽입, 삭제의 시간복잡도가
O(log n) - 그러나 이진 탐색 트리는 정렬된 데이터에는 취약하다.⇒ 최악의 경우 모든 데이터를 살펴야 할 수도 있어 시간복잡도가
O(n)이 된다. - → 오름차순이든 내림차순이든 정렬된 데이터가 입력되면 편향 트리(
skewed tree)가 생김
Indexed Binary Search Trees
-

- 각 노드에는 추가적인 필드 ‘LeftSize’라는 변수가 있음
- 이진 탐색 트리의 기능 뿐만 아니라 순위(rank)별 검색 및 삭제 작업이 가능
- LeftSize : 왼쪽 서브트리의 원소 수
LeftSize와 Rank
- 요소의 rank 즉, 순위는 오름차순 순서에 따른 위치를 가리킨다.rank(2) = 0rank(20) = 7

- rank(15) = 5
- [2, 6, 7, 8, 10, 15, 18, 20, 25, 30, 35, 40]

- x를 루트노드로 하는 서브트리의 요소에 대하여 LeftSize(x) = rank(x)
- indexed Binary Tree의 활용
insert(index, element)

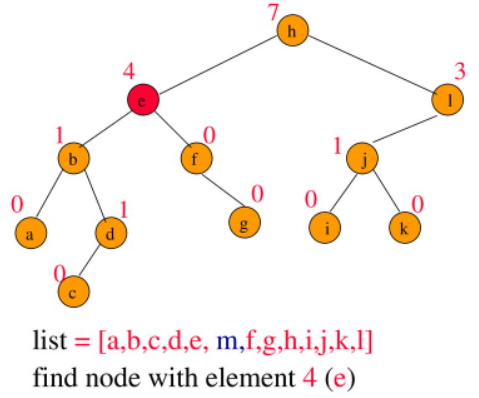


- 여러 가능성이 존재할 수 있다.
- 루트 노드부터 새로운 노드까지의 leftSize를 업데이트해야 한다.
- 시간 복잡도는 O(height)
Binary Search Tree with Duplicates
중복이 있는 이진 탐색 트리
이진 탐색 트리의 모든 요소에 별도의 key가 필요하다는 요구사항을 제거해볼 수 있다.
For every node x,
all keys in the left subtree of x are smaller than that in x.
all keys in the right subtree of x are larger than that in x
- “smaller” → "smaller or equal to"로,
- "larger" → "larger or equal to"으로 바꾼다.
그러면 이진 검색 트리가 중복 키를 가질 수 있게 된다.
참고자료
'Computer Science > Data Structure' 카테고리의 다른 글
| [자료구조] 레드 블랙 트리 (Red Black Tree) (0) | 2022.05.03 |
|---|---|
| [자료구조] AVL트리 (AVL Tree) (0) | 2022.05.03 |
| [자료구조] 스레드 이진 트리 (Threaded Binary Tree) (0) | 2022.04.26 |
| [자료구조] 트리 (Tree) (0) | 2022.04.26 |
| [자료구조] 연결리스트(Linked List) (0) | 2022.03.11 |













